Mit dieser Vortragsreihe möchte sich die Informatik erneut der Universitätsöffentlichkeit stellen. Sie tat dies bereits an einem eintägigen Festkolloquium am 24. April 1992; seitdem sind reichlich vier Jahre vergangen und es sind neue Kollegen in der Informatik hinzugekommen. Sicher läßt sich auch in einer Vortragsreihe über das ganze Wintersemester mehr sagen als an einem eintägigen Kolloquium, und sicher besteht dabei weniger die Gefahr, die Hörer zu überfordern. Lassen Sie mich zunächst ein paar Bemerkungen zum Titel der Vortragsreihe machen, in der wir (etwas selbstironisch überspitzt) das Selbstverständnis der Informatik ansprechen.

Ich erinnere mich an Diskussionen in einer Anhörung des Großen Senats der Eberhard-Karls-Universität, als es um die Einrichtung der Fakultät für Informatik ging; hier wurde unter anderem gefragt, welches denn die Rolle einer eher technischen Wissenschaft wie der Informatik an einer klassischen Universität sein könnte, in der sich [Zitat aus dem Gedächtnis] "die anderen Wissenschaften sämtlich mit Grundfragen der Welt und des Menschen" beschäftigten. Der Computer als Hauptgegenstand der Informatik dagegen sei doch ein artifizielles (und vielleicht vergängliches) Produkt. Wir finden dieses Wörtchen " artifiziell " in einer etwas anderen Wendung im Titel der Vortragsreihe wieder; das andere lateinische Wort " Calculemus " haben wir bei Leibniz entlehnt und möchten damit deutlich machen, daß die Informatik auch einen philosophischen Hintergrund hat. Dazu muß ich etwas ausholen.

In der angelsächsischen Literatur gibt es Diskussionen, ob diese Wissenschaft nun compu ter science oder comput ing science genannt werden muß, d.h. also ob sie tatsächlich primär mit dem Computer als einer universellen Maschine beschäftigt ist oder ob sie sich allgemein mit "Rechenprozessen" aller Art beschäftigt. Die zweite Alternative wirft sogleich das nächste Problem auf, nämlich zu definieren, was man unter einem "Rechen"prozeß verstehen will. Die deutsche Bezeichnung Informatik , die Anfang der sechziger Jahre in Anlehnung an den in Frankreich eingeführten Begriff informatique eingeführt wurde, vermeidet dieses Begriffsproblem bewußt und macht einerseits klar, daß wir uns hier mit Informationsverarbeitung im weitesten Sinne beschäftigen; andererseits halte ich aber auch den Gleichklang mit Mathematik durchaus nicht für einen Zufall. Manche Kollegen sehen Informatik in der Tat als einen Zweig der konstruktiven Mathematik; für sie ist Informatik in der Hauptsache die Wissenschaft von den Algorithmen (auf die wir noch zu sprechen kommen werden) . Andere sehen sie mehr in der elektrotechnischen Tradition und definieren sie deshalb als eine Ingenieurswissenschaft , die für ein Problem unter gegebenen Randbedingungen eine wirtschaftliche und sichere Lösung sucht. Wieder andere versuchen einen Kompromiß dazwischen und bezeichnen Informatik als eine allgemeine Methodenwissenschaft . Carl Friedrich von Weizsäcker schlug vor, Informatik ebenso wie Mathematik als eine Strukturwissenschaft anzusehen. Wir wollen hier nicht in eine wissenschaftstheoretische Debatte eintreten und wenden uns statt dessen zunächst einmal dem Computer zu.

Die ersten Metaphern, die zu Beginn der Fünfziger Jahre mit dem Computer verbunden wurden und sich teilweise erstaunlich lange gehalten haben, sind die des Elektronengehirns , des giant brain , der thinking machine . Hier wurde der Computer als der ultimative, weil unfehlbare und durch und durch rationale Denker charakterisiert, gegenüber dem der Mensch mit seinen Irrtümern notwendig als zweite Wahl erscheinen muß. Daß es zu einer derartigen Überschätzung des Computers kommen konnte, liegt vielleicht daran, daß dieser einen alten Menschheitstraum zu verwirklichen schien: Hier kommen wir auf den bereits erwähnten Begriff des Algorithmus zurück. Dieses scheinbar griechische Wort ist in Wirklichkeit von dem Namen des Mathematikers Mohammed ibn Musa abu Djafar al Khowarizmi (auch al Choresmi, ca. 783-850) aus Choresmien (im Gebiet des heutigen Usbekistan) abgeleitet, der in Bagdad in dem vom Kalifen Harun al Raschid gegründeten "Haus der Weisheit" zusammen mit anderen Wissenschaftlern Übersetzungen der griechischen mathematischen und medizinischen Schriften ins Arabische anfertigte und auf dieser Basis selbst weiter forschte. Er schrieb ein weitverbreitetes Buch mit dem arabischen Titel "Kitab al muhtasar fi hisab al gebr we al muqabala" ("Kurzgefaßtes Lehrbuch für die Berechnung durch Vergleich und Reduktion"), das bereits Lösungen von Gleichungen mit mehreren Unbekannten behandelte. In der lateinischen Übersetzung dieses Buchs, das durch die Kreuzfahrer nach Europa kam, begannen die Abschnitte jeweils mit "Dixit algorismi" ("So sprach al Khowarizmi"); daher der Name Algorithmus. Das besondere am Algorithmus ist es, daß er ein vielleicht kompliziertes mathematisches Verfahren in einer Weise in Einzelschritte zerlegt, daß man durch beharrliches Durchführen dieser Einzelschritte zu korrekten Lösungen kommt, auch wenn man das Verfahren als ganzes nicht verstanden hat, vom mathematischen Hintergrund einmal ganz zu schweigen. Damit wird die Möglichkeit für menschliche Irrtümer eingeschränkt und bereits die Basis für eine maschinelle, d.h. unintelligente Behandlung gelegt. In Spanien hatte Raimundus Lullus (Ramon Llull) im 13. Jahrhundert die Vision, daß es möglich sein müßte, mit Hilfe der von ihm erdachten ars combinatoria aus absoluten Prinzipien alle möglichen Begriffe herzuleiten; allerdings sind seine Ausführungen wenig präzise. Dieser Gedanke wurde 1666 von Leibniz aufgegriffen, der die ars inveniendi von der ars iudicandi unterschied. Mit der einen sollte es möglich sein, absolute Wahrheiten algorithmisch herzuleiten, mit der anderen, Aussagen zu verifizieren oder zu falsifizieren. Leibniz ging so weit ù und hier kommen wir wieder auf unseren Titel zurück ù zu prophezeien, daß sich in ferner Zukunft philosophische Dispute gänzlich erübrigen würden, weil die Philosophen sich in Zweifelsfällen auf ein " calculemus!" einigen würden: "Laßt es uns ausrechnen!". Leibniz "erfand" zwar die Dualzahlen, auf denen heutige Computer basieren und baute auch eine Rechenmaschine; den modernen programmgesteuerten Computer hat er jedoch vermutlich nicht ahnen können. Zwar hat die moderne Mathematik zu Anfang dieses Jahrhunderts mit ihren Unvollständigkeitssätzen bewiesen, daß Leibniz's Visionen unmöglich realisiert werden können, trotzdem hat der Computer ganz in der Leibnizschen Tradition einen absoluten Wahrheitsanspruch aufgrund seiner scheinbaren Objektivität und Rationalität. Computer fahren U-Bahnzüge billiger und sicherer als menschliche Fahrer, sie landen Flugzeuge im Nebel, planen Wartungsarbeiten am ICE, kurz: sie sind zuverlässige Befolger vorgegebener Regeln. Das hat schon in den sechziger Jahren unseres Jahrhunderts in weiten Kreisen zu einer gewissen Euphorie geführt, und hier kommen wir wieder auf die Vokabel "artifiziell": Die Vertreter der sog. "harten künstlichen Intelligenz" ("artificial intelligence") glaubten, daß man in der Lage sein würde, durch einen entsprechenden Satz von Regeln menschliche Intelligenz nachzubilden, ja womöglich zu übertreffen. Das sind Exzesse, die heute von ernstzunehmenden Informatikern nicht mehr mitgetragen werden.

Wie kommen wir aber von der artifiziellen Intelligenz auf die "artifiziellen Paradiese"? Beim freien Assoziieren über die teilweise überzogenen Verheißungen von scheinbar grenzenlosen Segnungen der Computertechnik erinnerte sich einer unserer Informatiker an dieses Buch von Baudelaire ("Les paradis artificiels", 1860). Hier dreht es sich um Bewußtseinserweiterung durch Wein, Opium und Haschisch, sicherlich eine besonders boshafte Verwendung des Worts "artifiziell". Manche geplagten Ehepartner von Computerfreaks können jedoch sicherlich auch in der Computerverwendung gewisse Suchtaspekte wiederfinden. Andererseits läßt sich der Begriff als solcher ohne Anspielung auf Baudelaire ganz aktuell neuinterpretieren vor dem Hintergrund der sog. "virtual reality", vermutlich eins der faszinierendsten Oxymorons, das dieses Jahrhundert hervorgebracht hat. Unser Kollege Straßer wird darüber vortragen.

Kommen wir jetzt jedoch zum eigentlichen Thema meines Vortrags. Als Tübinger haben wir alle genug Gustav Schwab gelesen, um bei diesem Titel sofort an die Geschichte von Herakles zu denken, der sich zwischen Tugend und Liederlichkeit zu entscheiden hatte:

Es fällt schwer, bei dieser Allegorie nicht an die theoretische Informatik und Windows-95 zu denken. Aber wir reden hier ja nicht von Herakles, sondern von dem Software-Ingenieur. Was haben wir uns denn unter einem Software-Ingenieur vorzustellen?

Als in den Sechzigern Computer langsam so leistungsfähig wurden, daß man außer mathematischen Verfahren auch größere Anwendungen "aus dem richtigen Leben" für sie programmieren konnte, wurden bald sehr große Softwaresysteme implementiert. Bereits damals bemerkte man rasch, daß der technologische Fortschritt bei der Software-Erstellung nicht mit den Hardware-Entwicklungen Schritt halten konnte: die Software wurde erst lange nach dem geplanten Termin fertig und war dann immer noch fehlerhaft; viele Projekte wurden vorzeitig aufgegeben. Man sprach allgemein von der "Software-Krise", die es zu besiegen galt. Schnell war dann auch der richtige Slogan gefunden: Wie man weiß, können Ingenieure auch sehr große Systeme auf eine Art planen und bauen, daß sie zum richtigen Termin unter den vorgegebenen Kosten fertig werden können und korrekt funktionieren. Man brauchte also "nur" die Software nach ingenieursmäßigen Methoden zu erstellen und alle Probleme waren gelöst. So entstand (1968) "Software Engineering", was wir auf deutsch mit Softwaretechnik bezeichnen.

Wir sind es von sonstigen Erzeugnissen der Ingenieurskunst, seien es nun Waschmaschinen, Autos, Fernseher, gewöhnt, daß die Hersteller eine gewisse Garantie für das korrekte Funktionieren des Produkts über einen gewissen Zeitraum übernehmen. Schaut man sich dagegen Garantiebestimmungen für Software an, so stellt man fest, daß hier in der Regel nicht viel mehr garantiert wird als daß die Disketten schwarz, quadratisch und mit magnetischen Aufzeichnungen versehen sind. Das einzige Recht, das dem Kunden eingeräumt wird, ist das Recht auf Rückzahlung des Kaufpreises.

Genüßlich berichten die Medien von Software-Desastern; manche sprechen von "Bananen-Software" (sie reift beim Kunden):

• Durch eine falsche Software gerät die für 11 Milliarden Mark entwickelte Ariane 5 außer Kontrolle und muß gesprengt werden.
• Neue Software im elektronischen Stellwerk Hamburg-Altona legt die Eisenbahn im Großraum Hamburg für zwei Tage lahm.
• Im neuen Flughafen Denver versagt die Softwaresteuerung der Gepäcktransportbänder derart, daß Koffer zerrissen werden. Der Flughafen wird mit 16-monatiger Verspätung eröffnet bei einem Verdienstausfall von rund einer Million Dollar pro Tag.
• In Warschau rast ein Airbus über die Landebahn hinaus und geht in Flammen auf, weil die Bordcomputer die Auslösung der Schubumkehr verweigerten.

Es wäre aber weit gefehlt, die Informatiker anzuschuldigen, sie hätten den Perfektionsgrad sonstiger Ingenieursdisziplinen noch nicht erreicht. In der Tat liegt es in der Natur des digitalen Computers, daß es ab einem gewissen Komplexitätsgrad geradezu unmöglich ist, korrekte Programme zu entwickeln. Die klassischen Methoden der Ingenieure, Systeme so lange in Teilsysteme zu zerlegen, bis man auf einem Niveau angelangt ist, wo die Korrektheit sozusagen ins Auge springt, funktioniert bei Software nämlich nicht: man sieht nicht, "wie die Zahnräder ineinandergreifen" und ganz entfernt liegende Stücke der Software können zu ungeahnten Interaktionen führen. David Parnas hat das in seinem Artikel über das SDI-Programm ausgeführt; hier fehlt der Raum, die Argumentation zu wiederholen.

Wie fehlerhaft ist die Software denn nun? Es gibt Untersuchungen von 1994, bei denen bis zu 25 Fehler pro tausend Programmzeilen gefunden wurden. Das klingt sehr viel, bedeutet aber, bezogen auf die Programmzeilen, nur eine Fehlerquote von 2,5 %. Wirklich gute Software hat heute etwa zwei bis drei Fehler pro tausend Zeilen, also eine Fehlerquote von zwei bis drei Promille. Es geht aber noch besser: Von einem Hersteller medizinischer Geräte weiß ich, daß dort nur ca. 2 Fehler pro zehntausend Zeilen gemacht werden; die Bord-Software für das Space Shuttle hat weniger als einen Fehler pro zehntausend Zeilen. Allerdings spricht man hier von Entwicklungskosten in der Gegend von 1000 Dollar pro Programmzeile; bei den drei Millionen Zeilen der Space-Shuttle-Software sind das drei Milliarden Dollar. Bei anderen Ingenieursprodukten sind meist viel größere Fehlertoleranzen im Gespräch, z.B. Geschwindigkeitsmesser von Autos dürfen 7% nach StVZO vom Skalenendwert voreilen. Endet der Tacho also bei 260 km/h, so dürfen bei einer wirklichen Geschwindigkeit von 50 km/h schon fast 70 km/h angezeigt werden. Wenn das die Fahrer einkalkulieren, fahren vermutlich alle zu schnell.

Ich möchte die Fehlerzahlen noch von einer anderen Seite her beleuchten, damit auch klar wird, was sie bedeuten. Ein digitales Handy beinhaltet heutzutage etwa 200000 Zeilen Programm, enthält also (unter der Voraussetzung guter Software) bis zu 600 Fehlern. Betrachtet man den Preis dieser Geräte, stellt man fest, daß wir etwa eine Mark pro Fehler zahlen. Das bekannte Produkt Windows-95 hat zehn Millionen Programmzeilen, würde also, wenn es gute Software wäre, zwischen 200000 und 300000 Fehlern enthalten. Wir erkennen hier das grundsätzliche Problem: Die Qualität der Software ist nicht so sehr das Problem wie ihre schiere Größe.

Ich möchte noch eine Lanze für die Programmierer brechen, indem ich die Fehlerzahlen noch in Relation zu einer anderen Zahl setze: Ein Programmierer schreibt im Durchschnitt ca. 100 Programmzeilen pro Woche, d.h. er braucht 10 Wochen, um die ominösen tausend Programmzeilen zu erstellen. Das bedeutet aber, daß er nur alle drei bis fünf Wochen einen einzigen Fehler begeht!

Aus der Industrie ist bekannt, daß bei sehr guter Software zwischen 25 und 185 Stunden für den Test von 1000 Programmzeilen aufgewendet werden; das bedeutet reine Testkosten zwischen 3250 und 24050 DM. Eine Alternative ist das Verifizieren : Wir schreiben eine formale Spezifikation für das Programm und beweisen mit Mitteln der mathematischen Logik, daß das Programm dieser Spezifikation entspricht. Kollege Reif in Ulm hat damit Erfahrung; mit Hilfe des KIV (Karlsruhe Interactive Verifier) kann ein Experte im Jahr zwischen 1000 und 2000 Zeilen Programm verifizieren. Zu BAT-Preisen sind das auch immerhin 100 bis 200 DM pro Zeile nur für die Verifikation; dafür ist die Software dann per definitionem fehlerfrei. Die Verifikation der Space-Shuttle-Software würde allerdings nach diesen Maßstäben einen Experten zwischen 1500 und 3000 Jahren beschäftigen.

Wir können mathematisch fehlerfreie Programme schreiben, aber das kostet Zeit und Mühe. Solches hat auch die Tugend dem Herakles angekündigt:

Trotzdem sind auch verifizierte, 100 % fehlerfreie Programme nicht immer korrekt im alltäglichen Sinne des Wortes. Dieser scheinbare Widerspruch erklärt sich dadurch, daß selbst die Elimination (z.B. durch Verifikation) aller Fehler bei der Umsetzung von Spezifikationen in Programme nicht verhindern kann, daß häufig bereits bei der Spezifikation Fehler gemacht werden, die manchmal erst nach längerer Betriebszeit und unter spezifischen Randbedingungen zutage treten und womöglich große Schäden hervorrufen.

Hier kommen wir auf das Problem der Abstraktion zu sprechen, das bei allen Programmen inhärent ist: um ein Problem mit dem Computer zu lösen, erstellen wir zunächst ein abstraktes mathematisches Modell. Letzten Endes werden alle Objekte, mit denen wir zu tun haben, in der einen oder anderen Weise auf Zahlen abgebildet, mit denen wir dann weiter hantieren, ohne immer an die dahinterstehenden Objekte denken zu müssen oder zu wollen. In der Informatik-I-Vorlesung habe ich dies immer an folgendem Beispiel vorgeführt:

Diese Aufgabe fand ich (mit festen Zahlen statt der Variablen n und m ) im Lambacher -Schweizer, dem klassischen Mathematikbuch für die Schule. Wir wollen für den Augenblick annehmen, daß diese Rätselaufgabe von so eminenter praktischer Bedeutung ist, daß jemand beauftragt wird, ein Programm hierfür zu schreiben. Dann werden mehr oder weniger folgende Überlegungen stattfinden: Offensichtlich ist die gesuchte Zahl P eine Funktion der Zahlen n und m , also P=P(n,m) . Gleiches gilt für die hier nicht erwähnte, aber implizit vorhandene Zahl M=M(n,m) der Motorräder. Offensichtlich ergibt P plus M die Gesamtzahl n der Fahrzeuge. Zieht man jetzt noch in Betracht, daß ein PKW 4 Räder hat und ein Motorrad 2, so ist klar, daß wir es, mathematisch gesprochen, mit der Lösung des folgenden linearen Gleichungssystems zu tun haben:

Wir lösen die erste Gleichung nach M auf und setzen das Ergebnis in die zweite Gleichung ein. Das führt zu der folgenden Rechnung:

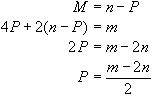
An dieser Stelle ist das Problem, so weit die Mathematik betroffen ist, bereits gelöst. Wir brauchen jetzt nur noch die Zahlen einzusetzen. Vielfach sind auch in dieser Weise mathematische Formeln in Programme umgesetzt worden, mit z.T. erschreckenden Ergebnissen. Aus der Frühzeit des Computereinsatzes sind die "Null-Mark-Rechnungen" bekannt, über die man sich so lange lustig machte, bis man dann auch noch eine Null-Mark-Mahnung bekam. Zuletzt konnte man manchmal das Problem nur noch durch eine fiktive Null-Mark-Überweisung beheben. Vergessen wurde nämlich hier in unserem Beispiel wie auch in anderen Fällen, daß die Mathematik nur zutreffende Aussagen über mathematische Objekte, z.B. Zahlen, macht und daß sie von PKW's, Rädern, Rechnungen und Mahnungen nichts weiß, nichts wissen kann und letzten Endes auch nichts wissen will. Bertrand Russell hat gesagt: "In der Mathematik wissen wir nie, wovon wir reden, und wenn wir es wissen, dann nicht, ob es wahr oder falsch ist." Ohne die in der Mathematik übliche Abstraktion kämen wir allerdings nicht sehr weit.

Verfolgen wir aber unser Beispiel weiter und nehmen an, daß nach der obigen Formel ein Programm für das "Parkplatzproblem" erstellt worden sei. Es ist Tradition, daß ein solches Programm getestet wird, d.h. man läßt es mit Probedaten laufen und stellt fest, ob das Ergebnis richtig oder zumindest glaubhaft ist. In unserem Beispiel seien die ersten Testdaten nun zufällig "3 Fahrzeuge und 9 Räder". Das Programm berechnet daraus

,

also müßten hier anderthalb PKW's stehen, was der täglichen Anschauung widerspricht. Es ist auch kaum ein Trost, daß eine Kontrollrechnung nachweist, daß ebenfalls anderthalb Motorräder auf diesem Parkplatz stehen! Offensichtlich ergibt die Formel höchstens dann einen Sinn, wenn die eingegebene Räderzahl gerade ist. Wir versuchen also ein "besseres" Beispiel: "5 Fahrzeuge, 2 Räder". Unser Programm berechnet dann:

,

m.a.W.: es fehlen 4 PKWs auf dem Parkplatz! Eine Kontrollrechnung ergibt, daß dafür 9 Motorräder auf dem Parkplatz stehen. 9 "positive Motorräder" plus 4 "negative PKW's" ergeben zusammen natürlich die 5 Fahrzeuge, die wir gezählt haben wollen. Man sieht, zu wie unnatürlichen Schlußfolgerungen die Mathematik uns hier zwingt, weil wir unser Problem nicht sorgfältig genug abstrahiert haben. Eine Folgerung aus diesem zweiten Testfall ist, daß wir doch bestimmt mindestens doppelt so viele Räder wie Fahrzeuge eingeben müssen. Ist damit aber schon alles getan? Wahrscheinlich nicht; unser Vertrauen in das Programm ist bereits schwer erschüttert. Versuchen wir einen letzten Testfall: "2 Fahrzeuge, 10 Räder". Das Programm rechnet:

,

was auf den ersten Blick jedenfalls nicht so schockierend aussieht wie bei den anderen beiden Testfällen. Insofern ist dieser Testfall sogar noch schlimmer, weil der Fehler nicht so brutal ins Auge springt. Hier muß man schon genauer auf die Daten schauen und sich fragen, wie es sein kann, daß 3 von 2 Fahrzeugen PKWs sind. Außerdem müßten die 3 PKWs ja 12 Räder haben und man fragt sich, wo denn 2 dieser Räder abgeblieben sind. Die Antwort ist natürlich, daß sie von einem negativen Motorrad geschluckt wurden, welches natürlich auch die Fahrzeugzahl wieder von 3 auf 2 herunterbringt.

Was ich mit diesem zugegebenermaßen simplen Beispiel demonstrieren wollte, ist, daß wir sehr viel genauer abstrahieren müssen, wenn wir von einem Programm behaupten, daß es Probleme der realen Welt lösen kann. Der großzügige Abstraktionsstil der Mathematik (und vielleicht auch der Physik), der bestrebt ist, möglichst viele Details zu unterdrücken, ist hier nicht angebracht. Das ist der Punkt, wo der Informatiker auf den Plan tritt, weil er hier nun tatsächlich gebraucht wird. Er wird als erstes eine Spezifikation des Problems erstellen, die vielleicht so aussieht:

An diesem Punkt zeigt eine weitere Überlegung, daß die hier spezifizierte Vorbedingung, die gerade so viel an "Weltwissen" formalisiert, wie für die Beschreibung dieses Problems nötig ist, tatsächlich ausreicht, um die Nachbedingung zu garantieren: Denn wenn m gerade ist, dann ist auch gerade und somit wird jedenfalls eine ganze Zahl sein. Aus folgt, daß und damit das ganze Ergebnis P nicht negativ sein wird. Schließlich folgt noch aus , daß und damit gilt; dann wird aber auch sein. Somit sind alle Möglichkeiten für unsinnige Ergebnisse ausgeschlossen.

Wir können also, nachdem die Spezifikation soweit abgeklärt ist, ruhig das oben angesprochene Programm schreiben. Allerdings ist es gute Informatik-Tradition, daß ein Programm selbst die Einhaltung seiner Vorbedingungen nachrechnet, sofern dies mit vertretbarem Aufwand möglich ist; wo nicht, hat das Programm gefälligst das errechnete Ergebnis einer Plausibilitätskontrolle zu unterziehen, bevor es dieses von sich gibt.

Meine Damen und Herren,
ich habe versucht, Ihnen zu zeigen, daß es sehr schwer ist, korrekte Programme zu schreiben, warum dies so ist bzw. so sein muß und daß die Hauptschwierigkeit nicht so sehr im Programmieren oder Testen liegt, sondern in der korrekten Modellierung und Abstraktion. Hier liegt der Unterschied zwischen Informatik und reiner Programmierfertigkeit: In der Informatik führen wir die Studenten auf einem zugegebenermaßen steinigen und unbequemen Weg auf die höheren Ebenen der Modellierung und Gestaltung von Systemen und Strukturen. Dazu sind theoretische Hintergründe ebenso nötig wie eine große Präzision in der Terminologie und ein scharfer Intellekt, der in der Lage ist, auch komplexe Zusammenhänge zu überblicken.

Was die Tugend zu Herakles sagte, könnte ebenso die Informatik zum Software-Ingenieur sagen, und damit schließt sich der Kreis: